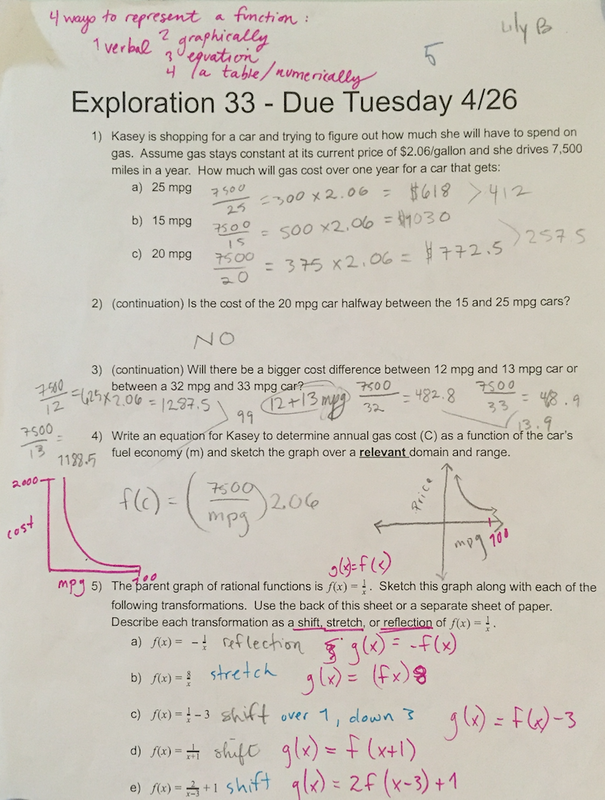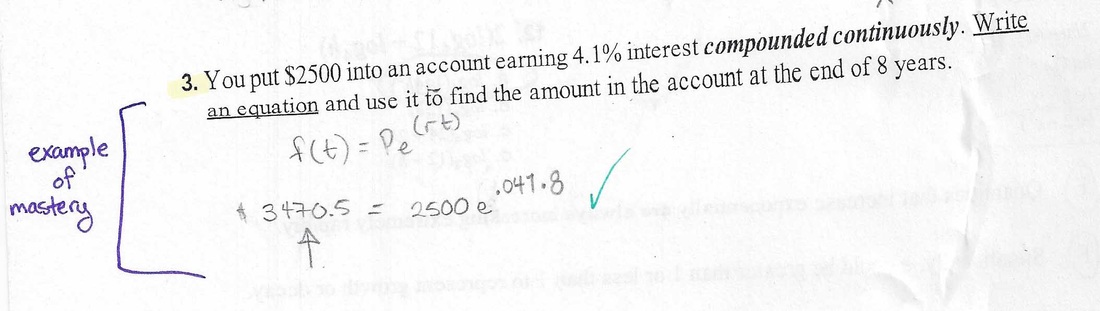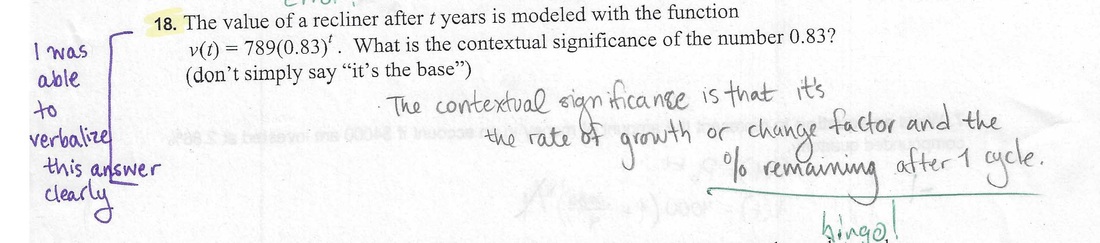ALGEBRA 2: SEMESTER 2 REFLECTION
|
Evidence for "Recognizing and resolving errors"
Evidence for "Reflecting and synthesizing"
|
HABITS OF A MATHEMATICIAN EVIDENCE AND REFLECTION
Generating ideas: I clearly showed my ability to generate ideas in my personal and independent Gear Ratio Spreadsheet. Within the spreadsheet I programmed different formulae and rules into the spreadsheet so the user had all the work done for them when they plugged in their individual numbers. I started by first researching how many teeth are on each chain-ring in order to formulate a plan to approaching how I would create this spreadsheet. Then I went into the mathematical side of calculating gear ratio and the corresponding distance you travel from any given gear ratio. I also found a way to calculate comparable gear ratios for a new sized bike, if you wanted to have a similar feel. After I played around with these equations and formulae and created them myself, I put them to use in my spreadsheet. Many of them didn’t work at first because of my lack of understanding of spreadsheets but after much refinement I ironed it all out and was able to learn a lot about spreadsheets and their different tricks. I used my ideas and problem solving skills to work through the struggles posed to me in the creation of the spreadsheet. Communicating thinking in a clear and accessible way: My demonstration of communication this year is seen in my Bike project. There were multiple times that I “responded to the ideas of others”, namely Dan. I came to a lot of standstills, first with the bike itself, as I was rebuilding it. I did not have certain parts in order to finish fixing it up. When I couldn’t continue work on the bike anymore, Dan helped brainstorm ideas with me about what route to take that still pertained to bikes and math. Together we decided I would start working on comparing and investigating the geometry of different bikes. I quickly began to lose interest in this subject as it was slightly monotonous with the direction I was going, so Dan suggested I study gear ratios. This was something that I worked at and understood. I came up with the idea to create a spreadsheet with different gear ratios and the corresponding distances you would travel with each pedal stroke. Without Dan’s help and original idea seed planting, I wouldn’t have accomplished as much especially because of my switch of focus throughout the project. My Bike Gear Ratio Spreadsheet can be seen here: https://docs.google.com/spreadsheets/d/1RdjsBCuBeuN0et59azecOJVYKzAuRkxBeSSzcaN1S3E/edit#gid=0 Recognizing and resolving errors: During this semester when we had seminar explorations I found myself developing a habit of marking my incorrect answers with a different colored pen. Not only would I put the correct answer but I would write out steps and helpful notes about the process. This aided me to understand each problem more fully as I went through the steps multiple times; at home, on the whiteboard with my seminar group and then again on my paper, if it was incorrect. It also proved helpful when I was reviewing my work for quizzes or as notes when I was looking for clarification on other problems. Reflecting and synthesizing: My reflection about my approach to a certain problem is evident in POW 10. I started out asking for help but after a small bit of clarity I did this problem myself and I understood it clearly. Aside from finishing and excelling at the problem solving process I wrote a clear and in depth reflection about my work in this POW. As I look back and read my reflection it is clear that I was confident and happy with my learning and performance in this POW. Being able to feel that 3 months later through a reflection I wrote about this problem makes me feel like that reflection and synthesizing was successful. |
ALGEBRA 2: SEMESTER 1 REFLECTION
Skills I have mastered...
During this semester I have learned how to identify and calculate exponential growth and decay in certain mathematical situations. An example of my work with this concept and evidence of my understanding of it is POW 5 and Practice 13. In POW 5 we were instructed to calculate how much would be left over after a certain amount of time. To do this we used the equation that we had come up for exponential growth and decay in class. This equation is: f(t)= Pb^kt. The definitions of these variables is the following: P= the initial value, b= is the change factor or the percent (%) remaining after 1 cycle, the variables in the exponents are, k=1/interval length and t= the input variable. This equation can help you when you are trying to figure out an amount after a specific amount of time as well as determining a time for a specific amount. Practice 13 shows my understanding and practice with this topic as we continued to elaborate and work with our knowledge by manipulating the variables to show us how they worked and related to each other. (see the pictures and annotations for more information)
This learning process was slow for me. When we were first taught exponential growth and decay I was confused and frustrated as it didn't make sense to me. It remained a rather foreign concept for a good couple weeks until one day I was sitting in class and it hit me, it made sense. The definitions of the variables and how to use the equation in a problem came together. At that moment I started POW 5 and with little assistance from Dan I finished the POW with full understanding of what I'd just done. I continued to understand it and that shows through on assignments and quizzes.
During this semester I have learned how to identify and calculate exponential growth and decay in certain mathematical situations. An example of my work with this concept and evidence of my understanding of it is POW 5 and Practice 13. In POW 5 we were instructed to calculate how much would be left over after a certain amount of time. To do this we used the equation that we had come up for exponential growth and decay in class. This equation is: f(t)= Pb^kt. The definitions of these variables is the following: P= the initial value, b= is the change factor or the percent (%) remaining after 1 cycle, the variables in the exponents are, k=1/interval length and t= the input variable. This equation can help you when you are trying to figure out an amount after a specific amount of time as well as determining a time for a specific amount. Practice 13 shows my understanding and practice with this topic as we continued to elaborate and work with our knowledge by manipulating the variables to show us how they worked and related to each other. (see the pictures and annotations for more information)
This learning process was slow for me. When we were first taught exponential growth and decay I was confused and frustrated as it didn't make sense to me. It remained a rather foreign concept for a good couple weeks until one day I was sitting in class and it hit me, it made sense. The definitions of the variables and how to use the equation in a problem came together. At that moment I started POW 5 and with little assistance from Dan I finished the POW with full understanding of what I'd just done. I continued to understand it and that shows through on assignments and quizzes.
Evidence of my mastery in this skill came out in my final Exponents and Logarithms Exam:
Habits of a Mathematician...
The two habits of a mathematician I have demonstrated the strongest this semester are 1) restating the problem in a different way that adds to my understanding and 2) translating my ideas using other forms or representations - language, symbolic, visual. I think that both these skills relate to to each other on a certain level. It is important to be able to see or explain concepts in a different way or with a new shed of light. I think that this habit can be translated to other aspects and areas of your life. I have demonstrated this throughout the year but again on my Exponents and Logarithms Exam I showed my understanding and ability to communicate this through my writing. Also in POW 7 I where I explained my process of solving the problem through writing as well.
The two habits of a mathematician I have demonstrated the strongest this semester are 1) restating the problem in a different way that adds to my understanding and 2) translating my ideas using other forms or representations - language, symbolic, visual. I think that both these skills relate to to each other on a certain level. It is important to be able to see or explain concepts in a different way or with a new shed of light. I think that this habit can be translated to other aspects and areas of your life. I have demonstrated this throughout the year but again on my Exponents and Logarithms Exam I showed my understanding and ability to communicate this through my writing. Also in POW 7 I where I explained my process of solving the problem through writing as well.
Exponents and Logarithms Exam Evidence:
POW 7 Evidence: see annotations and highlighting.