UNIT 3 REFLECTION: Area, Volume and Measurement
Questions 1&2: What skills/content have bee the most interesting to you?And how have these skills/content helped you grow mathematically?
Answer: During this unit I have touched up on a lot of skills and content that I have already learned, but it was nice to review them and learn them more in depth. It was interesting to me to learn volume and surface area. I feel I will use it in the future. I feel confident in my understanding of area and volume formulas. I don't know the surface area formulas as well, but I can use reasoning to figure them out. I was also really interested in the STATS function on our calculators. This was a very helpful tool in POW 5 when I had many data points and I was calculating the same formula to all of them. It is much easier to do it in a "batch" than one at a time. This function also helped me to organize my data in a table. I feel like this unit brought a lot of topics we have covered this year together and into one subject. It really helped me to approach problems in a different way, and to visualize new shapes and problems. An example of this is in POW 4 with the Rubik's cube. In this unit I feel I learned skills and content that I will use and will be helpful to know in the future.
Answer: During this unit I have touched up on a lot of skills and content that I have already learned, but it was nice to review them and learn them more in depth. It was interesting to me to learn volume and surface area. I feel I will use it in the future. I feel confident in my understanding of area and volume formulas. I don't know the surface area formulas as well, but I can use reasoning to figure them out. I was also really interested in the STATS function on our calculators. This was a very helpful tool in POW 5 when I had many data points and I was calculating the same formula to all of them. It is much easier to do it in a "batch" than one at a time. This function also helped me to organize my data in a table. I feel like this unit brought a lot of topics we have covered this year together and into one subject. It really helped me to approach problems in a different way, and to visualize new shapes and problems. An example of this is in POW 4 with the Rubik's cube. In this unit I feel I learned skills and content that I will use and will be helpful to know in the future.
UNIT 2 REFLECTION: Shadows, Similarity and Right Triangle Trigonometry
Question 1: What has been the work you are most proud of in this unit?
Answer: The work that I have been most proud of in this unit is my understanding of solving trigonometric ratios. I have learned and practiced when and how; tangent, sine or cosine formulas are used. By learning this I also learned how to use my calculator for these formulas. I show this understanding by the way I approach the problems and my confidence towards them. I feel that this was my strongest point in this unit.
Question 2:What skills are you developing in geometry/math?
Answer: I am developing many different skills in geometry that I can carry over to more math concepts in the future. One that I feel more confident about is combining different concepts to solve a problem. This may include using trig and area formulas in order to find the answer. I am also continuing to learn how to graph on my calculator and I have already learned so much about it. Once I master that skill it will be very helpful in the future. Another thing that I have learned and continue to master is drawing diagrams. When I don’t understand a problem, I draw it out. The problem or question automatically becomes more clear to me and I can then move on with the problem. I think that visual representation is really important and extremely helpful. I have learned a lot in this unit and I will carry what I’ve learned to future problems.
Question 3: Describe similarity (ratios) and it's real world application.
Answer: Similarity in Geometry is the way in which things relate to each other. If two shapes or objects are similar it means they have the same ratio but they may not be the same size. If a shape can be rotated, translated, shrunk or made bigger keeping the ratios of the sides the same, to become equal to another shape it is similar to that shape. Similarity is used to compare shapes, or to find a missing side length using ratios. A ratio is the way in which numbers relate to each other, it is a fraction. It is used in the real world when scaling art to make it larger or replicating statues. It is used when making models of things, they are smaller versions of a life size object or machine. Similarity is directly related to Trigonometry and it can be used to see how tall a building, miles away is. Similarity is used way more than we realize and without it we wouldn't have half the things we use today.
Answer: The work that I have been most proud of in this unit is my understanding of solving trigonometric ratios. I have learned and practiced when and how; tangent, sine or cosine formulas are used. By learning this I also learned how to use my calculator for these formulas. I show this understanding by the way I approach the problems and my confidence towards them. I feel that this was my strongest point in this unit.
Question 2:What skills are you developing in geometry/math?
Answer: I am developing many different skills in geometry that I can carry over to more math concepts in the future. One that I feel more confident about is combining different concepts to solve a problem. This may include using trig and area formulas in order to find the answer. I am also continuing to learn how to graph on my calculator and I have already learned so much about it. Once I master that skill it will be very helpful in the future. Another thing that I have learned and continue to master is drawing diagrams. When I don’t understand a problem, I draw it out. The problem or question automatically becomes more clear to me and I can then move on with the problem. I think that visual representation is really important and extremely helpful. I have learned a lot in this unit and I will carry what I’ve learned to future problems.
Question 3: Describe similarity (ratios) and it's real world application.
Answer: Similarity in Geometry is the way in which things relate to each other. If two shapes or objects are similar it means they have the same ratio but they may not be the same size. If a shape can be rotated, translated, shrunk or made bigger keeping the ratios of the sides the same, to become equal to another shape it is similar to that shape. Similarity is used to compare shapes, or to find a missing side length using ratios. A ratio is the way in which numbers relate to each other, it is a fraction. It is used in the real world when scaling art to make it larger or replicating statues. It is used when making models of things, they are smaller versions of a life size object or machine. Similarity is directly related to Trigonometry and it can be used to see how tall a building, miles away is. Similarity is used way more than we realize and without it we wouldn't have half the things we use today.
-PROBLEM OF THE WEEKS-
I personally have really enjoyed doing POWs. Through doing these I have learned how to problem solve on all different levels and it has helped me critically think. It has also developed my skill of breaking down problems. POWs can be very overwhelming and sometimes I don’t know where to start. I have learned to take a small part of the problem and go from there. It makes it less confusing. Although POWs don’t always directly relate to what we’re learning, they will definitely help me in the future when problem solving. Below are a few examples of my best POWs, I have collaborated with Skylar on one of them.
PROBLEM OF THE WEEK: FEBRUARY 3
PROBLEM OF THE WEEK: OCTOBER 29-NOVEMBER 4
GEOGEBRA: SNAIL TRAIL LAB
In this snail trail construction we started off with a hexagon construction, although we did it differently than we would normally construct it on paper. Then we reflected dots around the circle around each line. I then dragged point D in whatever way I wanted. When I moved point D around the circle, the reflectors followed each of their pair of reflectors. Ignoring the color this shape has reflectional and rotational symmetry involved. It also taught me a lot about GeoGebra, I feel a lot more confident and it’s a lot of fun. Math contributes to this by “reflections”and also equal distance between certain objects.
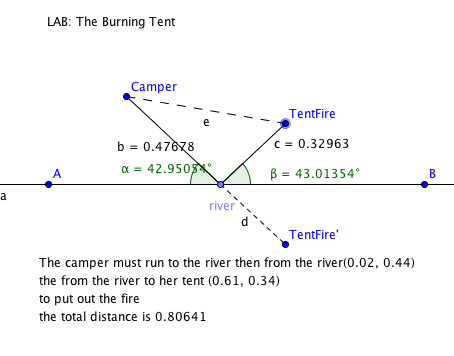
GEOGEBRA: THE BURNING TENT LAB
Question 1: Once you have a minimal path, what appears to be true about the incoming angle and the outgoing angle?
Answer: The ingoing and outgoing angles are almost equal, off by very small amounts.
Question 2: Why is the path from points Camper to TentFire' the shortest path? Briefly explain. (Think about the shortest distance between two points.)
Answer: It's the shortest because the angle of reflection is the same as the angle of the original point segment.
Question 3: Where should the point River be located in relation to segment Camper to TentFire' and line AB so that the sum of the distances is minimized?
Answer: It should be at the intersection of the line AB and the line segment.
Answer: The ingoing and outgoing angles are almost equal, off by very small amounts.
Question 2: Why is the path from points Camper to TentFire' the shortest path? Briefly explain. (Think about the shortest distance between two points.)
Answer: It's the shortest because the angle of reflection is the same as the angle of the original point segment.
Question 3: Where should the point River be located in relation to segment Camper to TentFire' and line AB so that the sum of the distances is minimized?
Answer: It should be at the intersection of the line AB and the line segment.